Cálculo é um ramo da matemática que explora variáveis e como elas mudam ao olhá-las em infinitamente pequenos pedaços chamados infinitesimais.
O cálculo, como é praticada hoje, foi inventado no século 17 pelo cientista britânico Isaac Newton (1642-1726) e pelo cientista alemão Gottfried Leibnitz (1646-1716), que desenvolveram de forma independente os princípios de cálculo nas tradições de geometria e matemática simbólica, respectivamente.Embora essas duas descobertas sejam mais importantes para o cálculo tal como é praticado hoje, não foram incidentes isolados. Pelo menos dois outros são conhecidos: Arquimedes (287-212 aC), na Grécia Antiga e Bhaskara II (1114-1185) na Índia medieval desenvolveram ideias de cálculo muito antes do século 17.
Tragicamente, a natureza revolucionária dessas descobertas ou não foram reconhecidas na época ou então estava tão enterradas noutras ideias novas e difíceis de entender que permaneceram quase esquecidas até aos tempos modernos.
A palavra "cálculo" tem uma origem modesta, decorrente de palavras semelhantes, como "calcular", mas todas estas palavras derivam de uma Latina (ou talvez ainda mais antiga) que significa "pedrinha". No mundo antigo, os cálculos eram feitos com pedras para manter o controle de gado e das reservas de grãos (ainda hoje, cálculos são pequenas pedras que se formam na vesícula biliar, rins ou outras partes do corpo).
A utilidade dos infinitesimais
Para compreender o que se entende por infinitesimal, considere a fórmula para a área de um círculo: A=πr². A demonstração a seguir é uma adaptação de uma dada pelo Professor Steve Strogatz de Cornell, que assinala que, apesar da simplicidade desta fórmula, ela é impossível de obter sem o uso de infinitesimais.
Para começar, reconhecemos que a circunferência de um círculo dividida pelo seu diâmetro (ou duas vezes o raio) é de cerca de 3.14, uma proporção denotada como o pi (π). Com esta informação, podemos escrever a fórmula para a circunferência de um círculo: C=2πr. Para determinar a área de um círculo, podemos começar por cortar o círculo em oito fatias de pizza e reorganiza-las da seguinte forma:
Conseguimos perceber que a margem curta, em linha reta é igual ao raio do círculo original (r), e o lado ondulado longo é igual a metade da circunferência do círculo (πr). Se repetirmos isso com 16 peças, fica reorganizado da seguinte forma:
Mais uma vez, vemos que a borda curta linear é igual ao raio da circunferência original (R), e o lado ondulado longo é igual à circunferência da metade do círculo (πr), mas o ângulo entre os lados é mais próximo de um ângulo recto e o lado mais longo é menos ondulado. Não importa o quanto aumentamos o número de peças do círculo, os lados curtos e longos mantêm os mesmos comprimentos e o ângulo entre os lados torna-se progressivamente mais próximo de um ângulo reto, e o lado longo torna-se progressivamente menos ondulado.
Agora, vamos imaginar que cortamos o círculo num número infinito de fatias. Na linguagem da matemática, as fatias são descritas como "infinitamente espessas", já que o número de fatias é levado ao limite do infinito. Neste limite, os lados ainda têm r e πr, mas o ângulo entre eles é realmente um ângulo reto e a ondulação do lado longo desaparece, o que significa que agora temos um rectângulo. O cálculo da área é neste caso apenas o comprimento x largura: πr × r = πr².
Duas metades de cálculo
O estudo de cálculo tem duas metades. A primeira metade, chamada cálculo diferencial, centra-se na análise de infinitesimais individuais e no que acontece dentro deles. A segunda metade, chamada cálculo integral, centra-se na adição de um número infinito de infinitesimais (como no exemplo acima).
Integrais e derivados são os opostos um do outro, sendo isso referido como o teorema fundamental do cálculo. Para explorar a forma como funciona vamos recorrer a um exemplo simples: Uma bola é lançada diretamente para o ar a partir de uma altura inicial de três pés e com uma velocidade inicial de 19,6 pés por segundo (ft/s). Se fizermos um gráfico com a posição vertical da bola ao longo do tempo, temos uma forma familiar conhecida como uma parábola.
Cálculo diferencial
Em todos os pontos ao longo desta curva, a bola está a mudar a velocidade, por isso não há período de tempo em que a bola esteja viajando a uma velocidade constante. Podemos, no entanto, encontrar a velocidade média durante qualquer período de tempo. Por exemplo, para encontrar a velocidade média de 0,1 segundos para 0,4 segundo, descobrimos a posição da bola nessas dois tempos e desenhamos uma linha entre eles.
Esta linha vai subir um pouco em comparação com a sua largura (o quão longe ele "corre"). Esta relação, muitas vezes referida como inclinação, é quantificado como altura ÷ tempo. Na posição de um gráfico em função do tempo, um declive representa a velocidade.
A linha sobe de 4,8 pés a 8,3 pés, mostrando um aumento de 3,5 pés. Da mesma forma, a linha vai de 0,1 segundo para 0,4 segundo num tempo de 0,3 segundos. A inclinação desta linha é a velocidade média da bola ao longo desta etapa da viagem: altura ÷ tempo = 3,5 pés ÷ 0,3 segundo = 11,7 pés por segundo (ft/sec).
Aos 0.1 segundos vemos que a curva é um pouco mais acentuada do que a média calculado, ou seja, a bola estava a mover-se um pouco mais rápido do que 11,7 pés/s. Da mesma forma, aos 0.4 segundos, a curva é um pouco mais nivelada, ou seja, a bola estava a mover-se um pouco mais lenta do que 11,7 pés/s. Se a velocidade se moveu de mais rápida para mais lenta significa que houve um instante no qual a bola realmente viajou a 11,7 pés/seg. Mas como podemos determinar o tempo exacto desse instante?
Se observarmos atentamente verificamos que o intervalo de 0,1 a 0,4 segundos não é o único período de tempo durante o qual a bola apresenta uma velocidade média de 11,7 pés/seg. Enquanto mantemos a inclinação da linha, podemos movê-la em qualquer lugar ao longo dessa curva e a velocidade média, durante o período de tempo entre os dois lugares da linha que intercepta a curva ainda será 11,7 pés/s.
Se mover a linha mais longe em direção à borda da parábola, o período de tempo diminui. Quando o período de tempo atinge o zero, os pontos pousam no mesmo local e a linha é dito ser tangente (apenas encostada) da parábola. O período de tempo é descrito como tendo sido "levado ao limite de zero".
É aqui que a noção de infinitesimais entra em jogo. Até este ponto, nós já conversamos sobre velocidade durante um período de tempo finito, mas agora estamos a falar de uma velocidade num instante; um período de tempo de duração infinitesimal. Observe como não podemos tomar o declive entre dois pontos que são infinitamente distantes uns dos outros; teríamos 0 pés ÷ 0 segundos, o que não faria qualquer sentido. Para encontrar a inclinação em qualquer ponto ao longo da curva, nós encontramos a inclinação da linha tangente. Os resultados de seis pontos são representados abaixo:
Este gráfico é o que é conhecido como derivado do gráfico original. Na linguagem da matemática e da física, diz-se que "o derivado da posição de um objeto em relação ao tempo é a velocidade desse objeto".
Cálculo integral
Este processo funciona em sentido inverso. O oposto de um derivado é um integral. Assim, "o integral da velocidade de um objecto com respeito ao tempo é a posição do objecto". Encontramos derivativos calculando encostas; encontramos integrais calculando áreas. Num gráfico da velocidade versus tempo, uma área representa um comprimento.
A questão de encontrar áreas num gráfico é relativamente simples quando se lida com triângulos e trapézios, mas quando os gráficos são curvas em vez de linhas retas, é necessário dividir uma área num número infinito de rectângulos com espessura infinitesimal (semelhante à forma como nós adicionamos um número infinito de cunhas infinitesimais para obter a área de um círculo).
Você deve ter notado que este gráfico integrante não chega a dar o mesmo gráfico vertical-posição com que nós começamos. Isso acontece porque ele é apenas um dos muitos gráficos das posições verticais que todos têm a mesma derivada. Algumas curvas semelhantes são mostrados abaixo:
Para determinar qual destas curvas nos dará o gráfico original da posição, também devemos usar algum conhecimento sobre a posição da bola num determinado momento. Exemplos disto incluem a altura da qual ela foi lançada (a posição vertical da bola no momento zero), ou o momento em que atingiu o solo (o tempo em que a posição vertical é zero). Isto é referido como uma condição inicial porque nós estamos geralmente preocupados em prever o que acontece depois. [Livescience]










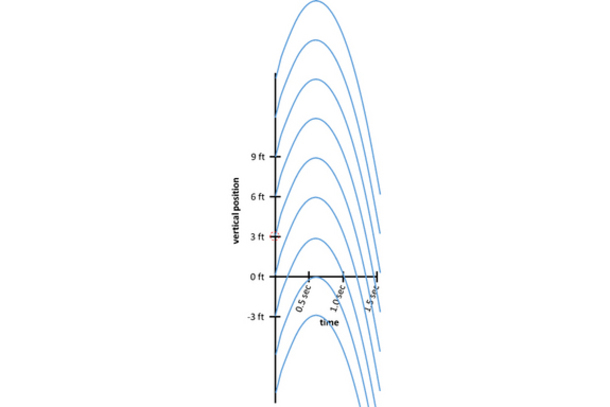

Mostre um exemplo gráfico com diferentes alturas de lançamento.
ResponderExcluir